Observables from Time-propagation TDDFT

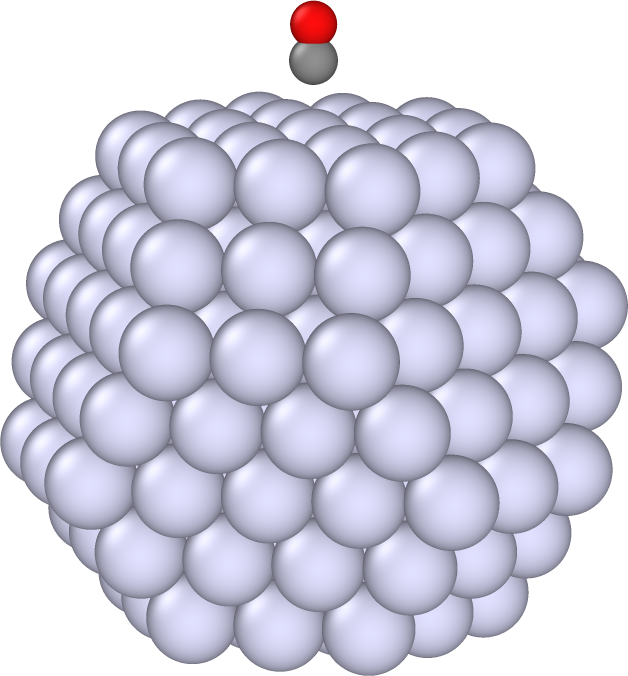
The file structure.xyz contains the structure of an Ag nanoparticle with the CO molecule approaching the (111) on-top site.

We read the file and set up an ground state calculation in GPAW.

• We use LCAO mode with the pvalence basis set (Kuisma et al. (2015); see here for installation)

• We use the GLLB-sc xc-functional to accurately describe the plasmonic response of Ag

The configuration options and details on how to run the calculation in parallel using MPI can be found in the GPAW documentation.

from ase.io import read
from ase.parallel import parprint

from gpaw import GPAW

atoms = read('structure.xyz')

# Add dipole moment corrections to center of metallic nanoparticle
metal_i = [sym in ['Na', 'Al', 'Ag', 'Au', 'Cu'] for sym in atoms.get_chemical_symbols()]
center = atoms.get_positions()[metal_i].mean(axis=0)
parprint(f'Center of NP is at {center}', flush=True)
moment_corrections = [dict(moms=list(range(1+3)), center=center)]

calc_kwargs = {}
calc_kwargs['mode'] = 'lcao'  # LCAO mode
calc_kwargs['h'] = 0.2  # Grid spacing in Å
calc_kwargs['setups'] = {'Ag': '11'}
calc_kwargs['basis'] = {elem: 'pvalence.dz' for elem in ['Ag', 'Au', 'Cu']}
calc_kwargs['poissonsolver'] = {'name': 'MomentCorrectionPoissonSolver',
                                'moment_corrections': moment_corrections,
                                'poissonsolver': 'fast'}
calc_kwargs['mixer'] = {'beta': 0.1, 'nmaxold': 5, 'weight': 50.0}
calc_kwargs['symmetry'] = {'point_group': False}  # Necessary for RT-TDDFT
calc_kwargs['occupations'] = {'name': 'fermi-dirac', 'width': 0.05}
calc_kwargs['maxiter'] = 450
calc_kwargs['xc'] = 'GLLBSC'
calc_kwargs['txt'] = 'gs.out'
calc_kwargs['parallel'] = {'sl_auto': True,
                           'augment_grids': True,
                           'domain': 1}  # Adjust to higher value if out of memory

calc_kwargs['nbands'] = -200
calc_kwargs['convergence'] = {'density': 1e-12, 'bands': -150}

# Set up calculator and converge ground state
calc = GPAW(**calc_kwargs)

atoms.calc = calc
atoms.get_potential_energy()

# Write the ground state to file
calc.write('gs.gpw', mode='all')

For later analysis, we will need to compute the KS wave functions in the full space, including all unoccupied states. We also construct a KohnShamDecomposition object to hold some additional information, like the dipole operator in the KS basis.

from ase.parallel import parprint
from gpaw import GPAW
from gpaw.lcaotddft.ksdecomposition import KohnShamDecomposition

gpwfile = 'gs.gpw'
gsunoccfile = 'gs_unocc.gpw'
ksdfile = 'ksd.ulm'

# Calculate ground state with full unoccupied space
parprint('Loading GS with full unoccupied space', flush=True)
calc = GPAW(gpwfile, fixdensity=True, nbands='nao')

calc.get_potential_energy()

parprint(f'Saving GS with full unoccupied space to {gsunoccfile}', flush=True)
calc.write(gsunoccfile, mode='all')

# Construct KS electron-hole basis
ksd = KohnShamDecomposition(calc)
ksd.initialize(calc)
ksd.write(ksdfile)
parprint(f'Saving Kohn-Sham decomposition to {ksdfile}', flush=True)

No we load the ground state file (the first file, with only the occupied states) and perform time propagation under some external field. We choose a spatially uniform (we are in the long-wavelength limit) field with a Gaussian temporal shape.

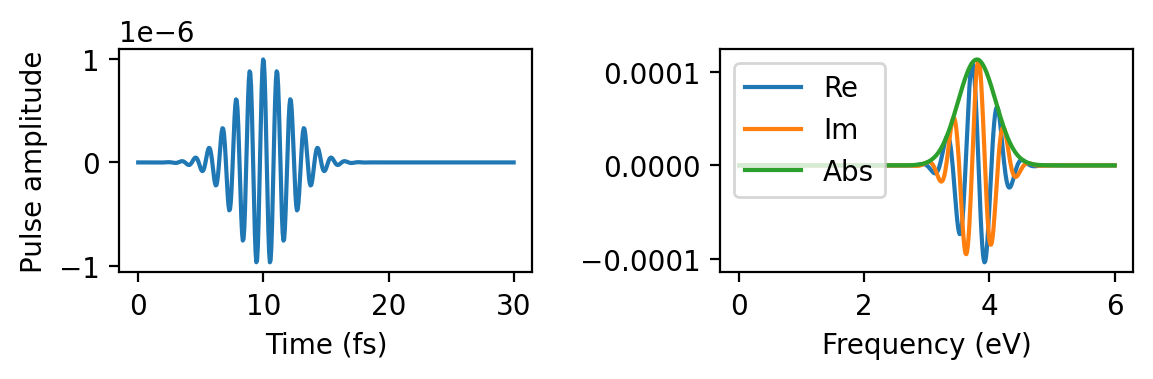
It is instructive to first plot the pulse

import numpy as np
from gpaw.tddft.units import eV_to_au, fs_to_au, au_to_fs
from matplotlib import pyplot as plt
from gpaw.lcaotddft.laser import GaussianPulse

def create_pulse():
    strength = 1e-6  # Amplitude
    time0 = 10e3  # Time of maximum in attoseconds
    frequency = 3.8  # Frequency in eV
    sigma = 0.3  # Width parameter in eV

    # Transform the sigma parameter of the Gaussian to a full-width at half-maximum
    fwhm_eV = np.sqrt(8 * np.log(2)) * sigma
    fwhm_fs = np.sqrt(8 * np.log(2)) / (sigma * eV_to_au) * au_to_fs

    print(f'Full width at half-maximum in time {fwhm_fs:.2f}fs')
    print(f'Full width at half-maximum in frequency {fwhm_eV:.2f}eV')

    # Temporal shape of the time-dependent potential
    pulse = GaussianPulse(strength, time0, frequency, sigma, 'cos')

    return pulse

fig, axes = plt.subplots(1, 2, figsize=(6, 2), dpi=200)

time = np.linspace(0, 30, 500)  # Time grid in femtoseconds for plotting
frequency = np.linspace(0, 6, 500)  # Frequency grid in eV for plotting
pulse = create_pulse()

axes[0].plot(time, pulse.strength(time * fs_to_au))
axes[0].set_xlabel('Time (fs)')
axes[0].set_ylabel('Pulse amplitude')

axes[1].plot(frequency, pulse.fourier(frequency * eV_to_au).real, label='Re')
axes[1].plot(frequency, pulse.fourier(frequency * eV_to_au).imag, label='Im')
axes[1].plot(frequency, np.abs(pulse.fourier(frequency * eV_to_au)), label='Abs')
axes[1].set_xlabel('Frequency (eV)')
axes[1].legend(loc='upper left')

fig.tight_layout()

Full width at half-maximum in time 5.17fs
Full width at half-maximum in frequency 0.71eV

Now we perform the time propagation. This is our most time consuming task. It is highly advisable to split the calculation into several shorter running jobs by writing to a restart file, and later restarting. We refer to the GPAW documentation on how to run using MPI and restart files.

• We attach a DipoleMomentWriter that writes the dipole moment at every timestep to dm_gauss.dat

• We attach a WaveFunctionWriter that writes the LCAO wave function coefficients to wfs_gauss.ulm. To save space, we write it every 10 steps

import numpy as np
from ase.units import Hartree, Bohr
from gpaw.external import ConstantElectricField
from gpaw.lcaotddft import LCAOTDDFT
from gpaw.lcaotddft.laser import GaussianPulse
from gpaw.lcaotddft.dipolemomentwriter import DipoleMomentWriter
from gpaw.lcaotddft.wfwriter import WaveFunctionWriter

# Temporal shape of the time-dependent potential
pulse = create_pulse()
# Spatial shape of the time-dependent potential
ext = ConstantElectricField(Hartree / Bohr, [0., 0., 1.])
# Time-dependent potential
td_potential = {'ext': ext, 'laser': pulse}

# Set up the time-propagation calculation
td_calc = LCAOTDDFT('gs.gpw',
                    td_potential=td_potential,
                    parallel={'sl_auto': True,
                              'augment_grids': True,
                              'domain': 1},  # Adjust to higher value if out of memory
                    txt='td_gauss.out')

# Attach the data recording and analysis tools
DipoleMomentWriter(td_calc, 'dm_gauss.dat')
WaveFunctionWriter(td_calc, 'wfs_gauss.ulm', interval=10)

# Propagate
td_calc.propagate(20, 1500)  # 1500 steps of 20 as

Analyzing the induced dipole moment

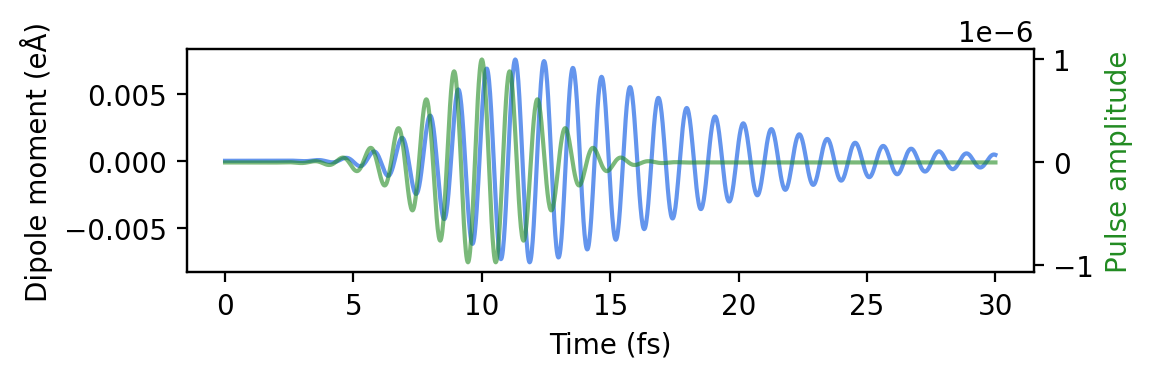
Let us plot the induced dipole moment by reading the dm_gauss.dat file. The system responds to the applied pulse by oscillating strongly. After the pulse has reached its maximum, however, the dipole moment of the system keeps oscillating. The amplitude of the oscillations slowly decreases over the remainder of the calculation.

from ase.units import Bohr

# Format of the file is (time, norm, dmx, dmy, dmz)
data = np.loadtxt('dm_gauss.dat')

time = data[:, 0] * au_to_fs  # Convert from atomic units to femtoseconds
dipmom = data[:, 4] * Bohr  # Convert from atomic units to eÅ

pulse = create_pulse()

fig, ax = plt.subplots(1, 1, figsize=(6, 2), dpi=200)
twinax = ax.twinx()

twinax.plot(time, pulse.strength(time * fs_to_au), color='forestgreen', alpha=0.6)
ax.plot(time, dipmom - dipmom[0], color='cornflowerblue')

ax.set_xlabel('Time (fs)')
ax.set_ylabel('Dipole moment (eÅ)')
twinax.set_ylabel('Pulse amplitude', color='forestgreen')

fig.tight_layout()

Full width at half-maximum in time 5.17fs
Full width at half-maximum in frequency 0.71eV

Let us analyze the system at a moment in time when the oscillations are large. The dipole moment can be expressed as

\[\boldsymbol{d}(t) = -2\sum_{ia} \boldsymbol{d}_{ia} \mathrm{Re}\rho_{ia}(t),\]

where \(\boldsymbol{d}_{ia}\) is the dipole operator in the basis of ground state Kohn-Sham (KS) orbitals, and \(\rho_{ia}(t)\) the KS-density matrix in the basis of ground state KS orbitals. The sum over \(ia\) goes only over states such that the occupation of \(i\) is larger than the occupation of state \(a\). By calculating and plotting \(\boldsymbol{d}_{ia} \rho_{ia}(t)\) we can find out which the states contribute the most to the dipole moment. The dipole matrix is \(\boldsymbol{d}_{ia}\) is stored in ksd.ulm, which we have already computed.

We set up a ResponseFromWaveFunctions object that tells rhodent how \(\rho_{ia}(t)\) can be computed. We initialize this object with the filename of the KohnShamDecomposition file and the file name of the wave function dump file.

For the purpose of visualization, we want to construct a transition contribution map where the discrete matrix elements \(\boldsymbol{d}_{ia} \rho_{ia}(t)\) are broadened onto an energy grid

\[\boldsymbol{d}(t, \varepsilon_o, \varepsilon_u) = -2 \sum_{ia} \boldsymbol{d}_{ia} \rho_{ia}(t) G(\varepsilon_i - \varepsilon_o; \sigma) G(\varepsilon_a - \varepsilon_u; \sigma)\]

by convolution with Gaussians \(G(\varepsilon_i - \varepsilon_o; \sigma)\) of width \(\sigma\) centered on the KS eigenenergies \(\varepsilon_i\).

We use the DipoleCalculator to calculate the product \(\boldsymbol{d}_{ia} \rho_{ia}(t)\) and broaden it on the energy grid. We give the DipoleCalculator the response object, a list of times \(t\), in attoseconds, for which we want to compute the observables, occupied and unoccupied energy grids \(\varepsilon_o\) and \(\varepsilon_u\) for the, and a \(\sigma\) parameter of 0.07eV. The calculator will choose times that are present in the wave function dump, and that are as close as possible to the specified times.

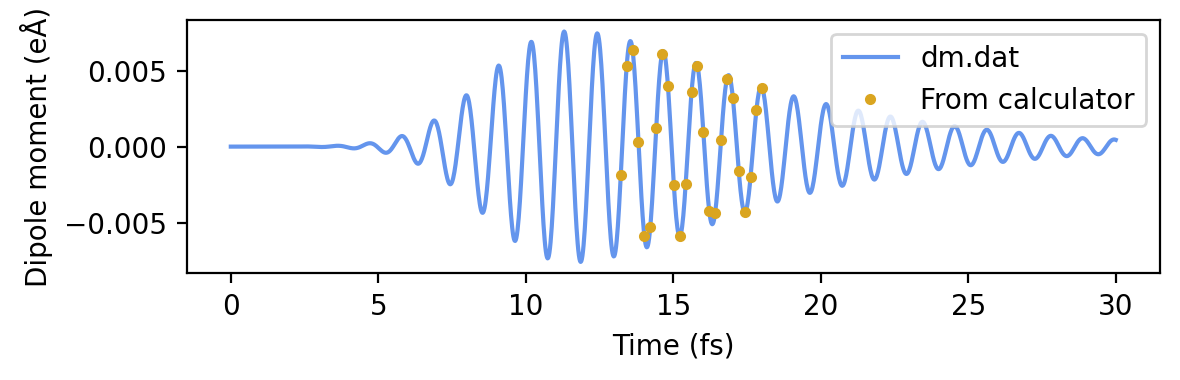
Finally we use icalculate_gather_on_root(yield_total_ou=True, v=2) to iteratively compute this quantity for each time and the \(z\) (v=2) component. In general, this function is able to work in parallel across many MPI ranks, and broadcast the results to only the root rank. Since we have only specified one time, it will only yield one result. We obtain the broadened grid from res['dm_ou'] and the actual time from metadata.time.

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import Normalize

from rhodent.response import ResponseFromWaveFunctions
from rhodent.calculators import DipoleCalculator

# Set up the density matrices object
response = ResponseFromWaveFunctions(
    ksd='ksd.ulm',
    wfs_fname='wfs_gauss.ulm')

# Set up the dipole calculator that calculates and broadens dipole contributions onto an energy grid
calc = DipoleCalculator(response,
                        times=np.arange(13100, 18000, 100),
                        energies_occ=np.arange(-5, 1, 0.01),
                        energies_unocc=np.arange(-1, 5, 0.01),
                        sigma=0.07)

time_from_calc = calc.times * 1e-3
dipmom_from_calc = []
# Iterate over the results
for metadata, res in calc.icalculate_gather_on_root(v=2):
    dipmom_from_calc.append(res['dm'])

[0000/0001] [00:00:00.0] Opened item #0
[0000/0001] [00:00:00.1] Opened item #100
[0000/0001] [00:00:00.3] Set up calculator:
=========== DipoleCalculator ===========
response:
  ResponseFromWaveFunctions
    ksd: ksd.ulm
    wfs_fname: wfs_gauss.ulm
    perturbation:
      No perturbation

voronoi:
  No Voronoi decomposition

Energies for broadening (sigma = 0.1 eV)
  Occupied: 600 from -5.0 to 1.0 eV
  Unoccupied: 600 from -1.0 to 5.0 eV
----------------------------------------
[0000/0001] [00:00:00.4] (on 1 ranks) Constructing C0_sknM
[0000/0001] [00:00:22.0] (on 1 ranks) Constructed C0_sknM
[0000/0001] [00:00:22.0] (on 1 ranks) Constructing rho0_skMM
[0000/0001] [00:00:35.3] (on 1 ranks) Constructed rho0_skMM
[0000/0001] [00:00:44.3] Calculated and broadened dipoles contributions in 0.02s for 13220.0as
[0000/0001] [00:00:53.3] Calculated and broadened dipoles contributions in 0.02s for 13420.0as
[0000/0001] [00:01:02.3] Calculated and broadened dipoles contributions in 0.02s for 13620.0as
[0000/0001] [00:01:11.5] Calculated and broadened dipoles contributions in 0.01s for 13820.0as
[0000/0001] [00:01:20.5] Calculated and broadened dipoles contributions in 0.02s for 14020.0as
[0000/0001] [00:01:29.5] Calculated and broadened dipoles contributions in 0.02s for 14220.0as
[0000/0001] [00:01:38.5] Calculated and broadened dipoles contributions in 0.02s for 14420.0as
[0000/0001] [00:01:47.5] Calculated and broadened dipoles contributions in 0.02s for 14620.0as
[0000/0001] [00:01:56.5] Calculated and broadened dipoles contributions in 0.02s for 14820.0as
[0000/0001] [00:02:05.6] Calculated and broadened dipoles contributions in 0.02s for 15020.0as
[0000/0001] [00:02:14.6] Calculated and broadened dipoles contributions in 0.02s for 15220.0as
[0000/0001] [00:02:23.5] Calculated and broadened dipoles contributions in 0.02s for 15420.0as
[0000/0001] [00:02:32.5] Calculated and broadened dipoles contributions in 0.02s for 15620.0as
[0000/0001] [00:02:41.5] Calculated and broadened dipoles contributions in 0.02s for 15820.0as
[0000/0001] [00:02:50.5] Calculated and broadened dipoles contributions in 0.02s for 16020.0as
[0000/0001] [00:02:59.6] Calculated and broadened dipoles contributions in 0.02s for 16220.0as
[0000/0001] [00:03:08.5] Calculated and broadened dipoles contributions in 0.02s for 16420.0as
[0000/0001] [00:03:17.5] Calculated and broadened dipoles contributions in 0.02s for 16620.0as
[0000/0001] [00:03:26.5] Calculated and broadened dipoles contributions in 0.02s for 16820.0as
[0000/0001] [00:03:35.5] Calculated and broadened dipoles contributions in 0.02s for 17020.0as
[0000/0001] [00:03:44.5] Calculated and broadened dipoles contributions in 0.02s for 17220.0as
[0000/0001] [00:03:53.6] Calculated and broadened dipoles contributions in 0.02s for 17420.0as
[0000/0001] [00:04:02.6] Calculated and broadened dipoles contributions in 0.02s for 17620.0as
[0000/0001] [00:04:11.5] Calculated and broadened dipoles contributions in 0.02s for 17820.0as
[0000/0001] [00:04:20.6] Calculated and broadened dipoles contributions in 0.02s for 18020.0as
[0000/0001] [00:04:20.6] Finished calculating dipoles contributions

# Plot the dipole moment and the dipole moment contributions
fig, ax = plt.subplots(1, 1, figsize=(6, 2), dpi=200)
ax.set_xlabel('Time (fs)')
ax.set_ylabel('Dipole moment (eÅ)')

ax.plot(time, dipmom - dipmom[0], color='cornflowerblue', label='dm.dat')
ax.plot(time_from_calc, np.array(dipmom_from_calc), '.', color='goldenrod', label='From calculator')
ax.legend()

fig.tight_layout()

# Get only the first result without recreating the calculator object
for metadata, res in calc.icalculate_gather_on_root(yield_total_ou=True, v=2):
    tcm = res['dm_ou']
    break

[0000/0001] [00:04:34.6] Calculated and broadened dipoles contributions in 4.96s for 13220.0as

# Plot the dipole moment and the dipole moment contributions
fig, ax = plt.subplots(1, 1, figsize=(4, 3), dpi=200)

p = ax.pcolormesh(calc.energies_occ, calc.energies_unocc, tcm.T, cmap='seismic', norm=Normalize(-0.02, 0.02))
ax.set_title(f'Time {metadata.time*1e-3:.1f}fs')
ax.axis('equal')
fig.colorbar(p, ax=ax, label='Dipole contributions (eÅ/eV$^2$)')


ax.set_ylabel('Energy electrons (eV)')
ax.set_xlabel('Energy holes (eV)')

fig.tight_layout()

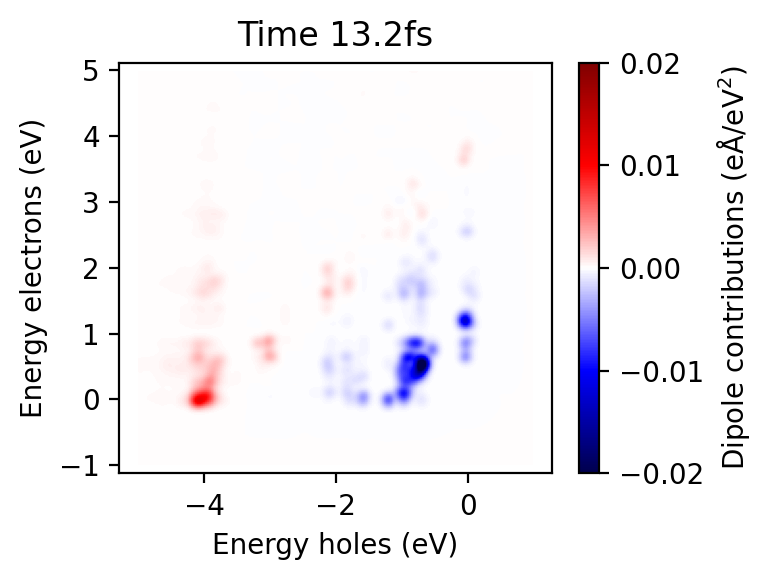
The calculation of density matrices and construction of TCMs takes some time, even if it is orders of magnitudes faster than the time propagation. It is useful to perform the calculation and write the results to a file. This is done using the calculate_and_write function. The ULM file format is useful for writing large matrices without having to store them entirely in memory.

import numpy as np

from rhodent.response import ResponseFromWaveFunctions
from rhodent.calculators import DipoleCalculator

# Set up the density matrices object
response = ResponseFromWaveFunctions(
    ksd='ksd.ulm',
    wfs_fname='wfs_gauss.ulm')

# Set up the dipole calculator that calculates and broadens dipole contributions onto an energy grid
calc = DipoleCalculator(response,
                        times=[6200],
                        energies_occ=np.arange(-5, 1, 0.01),
                        energies_unocc=np.arange(-1, 5, 0.01),
                        sigma=0.07)

# Calculate the transition contribution map and save it to a file
calc.calculate_and_write('tcm_gauss.ulm')

[0000/0001] [00:00:00.0] Opened item #0
[0000/0001] [00:00:00.1] Opened item #100
[0000/0001] [00:00:00.3] Set up calculator:
=========== DipoleCalculator ===========
response:
  ResponseFromWaveFunctions
    ksd: ksd.ulm
    wfs_fname: wfs_gauss.ulm
    perturbation:
      No perturbation

voronoi:
  No Voronoi decomposition

Energies for broadening (sigma = 0.1 eV)
  Occupied: 600 from -5.0 to 1.0 eV
  Unoccupied: 600 from -1.0 to 5.0 eV
----------------------------------------
[0000/0001] [00:00:00.4] (on 1 ranks) Constructing C0_sknM
[0000/0001] [00:00:22.2] (on 1 ranks) Constructed C0_sknM
[0000/0001] [00:00:22.2] (on 1 ranks) Constructing rho0_skMM
[0000/0001] [00:00:35.3] (on 1 ranks) Constructed rho0_skMM
[0000/0001] [00:00:44.2] Calculated and broadened dipoles contributions in 0.02s for 6220.0as
[0000/0001] [00:00:44.2] Finished calculating dipoles contributions
Written tcm_gauss.ulm

Analyzing the hot-carrier populations

The diagonals of the KS density matrix can be interpreted as the population of ground state KS orbitals. We use the calculate_hcdist_and_write function to calculate these and save to a file that we later plot.

By using a file name with the ‘.dat’ extension, it is formatted as a space-separated text file. Alternatively, you can provide the ‘.npz’ extension to save as a numpy archive.

from rhodent.response  import ResponseFromWaveFunctions
from rhodent.calculators import HotCarriersCalculator

# Set up the density matrices object
response = ResponseFromWaveFunctions(
    ksd='ksd.ulm',
    wfs_fname='wfs_gauss.ulm')

# Set up the hot-carriers calculator that calculates and broadens dipole contributions onto an energy grid
calc = HotCarriersCalculator(response,
                        times=[6200, 12000, 20000, 30000],
                        energies_occ=np.arange(-5, 1, 0.01),
                        energies_unocc=np.arange(-1, 5, 0.01),
                        sigma=0.07)

# Calculate the hot carrier distributions and save them to a file
calc.calculate_hcdist_and_write('hcdist_gauss.dat', average_times=False)

[0000/0001] [00:00:00.0] Opened item #0
[0000/0001] [00:00:00.1] Opened item #100
[0000/0001] [00:00:00.3] Set up calculator:
======== HotCarriersCalculator =========
response:
  ResponseFromWaveFunctions
    ksd: ksd.ulm
    wfs_fname: wfs_gauss.ulm
    perturbation:
      No perturbation

voronoi:
  No Voronoi decomposition

Energies for broadening (sigma = 0.1 eV)
  Occupied: 600 from -5.0 to 1.0 eV
  Unoccupied: 600 from -1.0 to 5.0 eV
----------------------------------------
[0000/0001] [00:00:00.4] (on 1 ranks) Constructing C0_sknM
[0000/0001] [00:00:21.9] (on 1 ranks) Constructed C0_sknM
[0000/0001] [00:00:21.9] (on 1 ranks) Constructing rho0_skMM
[0000/0001] [00:00:35.0] (on 1 ranks) Constructed rho0_skMM
[0000/0001] [00:00:44.3] Calculated and broadened HC distributions in 44.31s for 6220.0as
[0000/0001] [00:00:53.7] Calculated and broadened HC distributions in 53.73s for 12020.0as
[0000/0001] [00:01:03.2] Calculated and broadened HC distributions in 63.16s for 20020.0as
[0000/0001] [00:01:12.5] Calculated and broadened HC distributions in 72.46s for 29820.0as
[0000/0001] [00:01:12.5] Finished calculating hot-carrier matrices
Written hcdist_gauss.dat

!head hcdist_gauss.dat

# Hot carrier (H=hole, E=electron) distributions relative to Fermi level
# Computed for the following 4 times (in fs)
#   6.2200
#   12.0200
#   20.0200
#   29.8200
# Gaussian folding, Width 0.0700eV
# H energy (eV)   E energy (eV)     Total H (1/eV)     Total E (1/eV)  ... repeated for next times
      -5.000000       -1.000000     5.31310255e-11     4.35997202e-49     1.11674953e-08     6.32439939e-47     1.81085999e-09     1.46217358e-46     2.55043922e-10     1.52320464e-46
      -4.990000       -0.990000     5.45656737e-11     2.93354739e-48     1.14194576e-08     4.26023582e-46     1.85861158e-09     9.84538687e-46     2.59895514e-10     1.02547007e-45

from matplotlib import pyplot as plt

fig, axes = plt.subplots(1, 2, sharey=True, figsize=(6, 3), dpi=200)

data = np.loadtxt('hcdist_gauss.dat')
energies_occ = data[:, 0]
energies_unocc = data[:, 1]

times = [6.21, 12.01, 20.01, 30.01]
for t, time in enumerate(times):
    hcdist_o = data[:, 2 + 2 * t]
    hcdist_u = data[:, 3 + 2 * t]
    axes[0].plot(energies_occ, hcdist_o, label=f'Time {time:.1f}fs')
    axes[1].plot(energies_unocc, hcdist_u)

axes[0].set_ylabel('Carrier distribution (1/eV)')
axes[0].set_xlabel('Energy holes (eV)')
axes[1].set_xlabel('Energy electrons (eV)')
axes[0].legend()

fig.tight_layout()

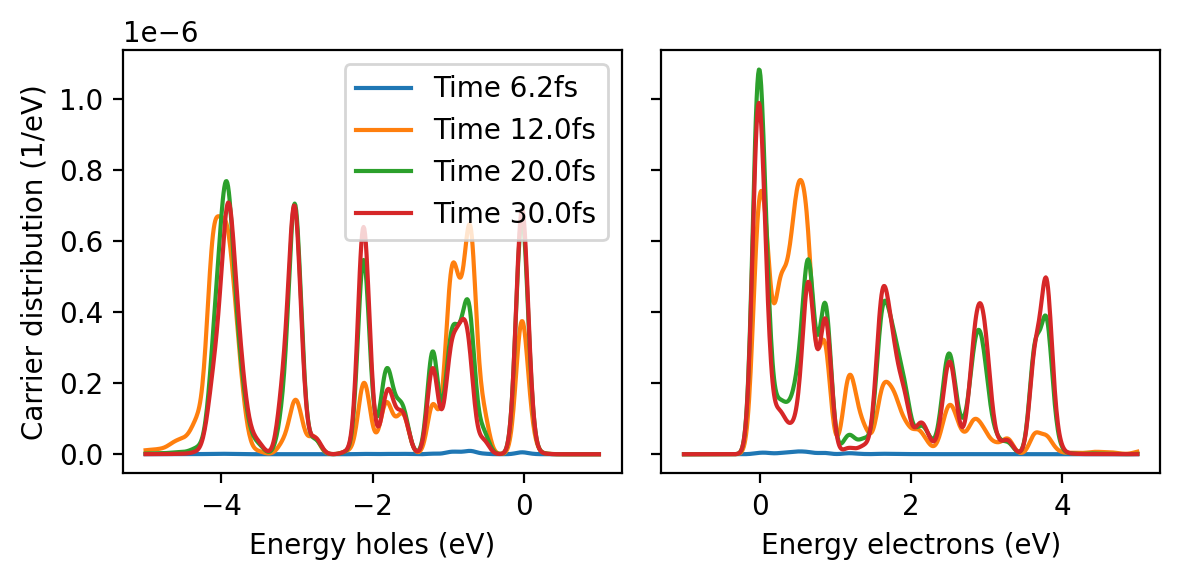
Where are the hot carriers localized?

Since we have the density matrix, we can decompose it by any means we want. The calculators support projection on ground state KS states according to a Voronoi weight. This weight is defined

\[w_{nn'} = \int_\text{partition} \psi_n(\boldsymbol{r})\psi_{n'}(\boldsymbol{r})\mathrm{d}\boldsymbol{r},\]

where the intergral is taken in the Voronoi partition of one or several atoms in space.

Compute the Voronoi decomposition of weights on the carbon and oxygen atoms, which are numbered 201 and 202, using the VoronoiWeightCalculator and VoronoiLCAOWeightCalculator. Save the decomposition to a file voronoi.ulm using calculate_and_save_by_filename. Then we load the voronoi weights using the VoronoiReader and pass it to the calculate_hcdist_and_write function.

Alternatively, it is also possible to calculate the weights on the fly by passing the VoronoiWeightCalculator directly to the calculator.

from rhodent.voronoi import VoronoiWeightCalculator, VoronoiLCAOWeightCalculator
from rhodent.writers.voronoi import calculate_and_save_by_filename

voronoi_lcao = VoronoiLCAOWeightCalculator([[201, 202]], 'gs_unocc.gpw', domain=1, use_pblas=True)
voronoi = VoronoiWeightCalculator(voronoi_lcao, use_pblas=True)

calculate_and_save_by_filename('voronoi.ulm', voronoi=voronoi)

[0000/0001] [00:00:00.0] Start
[0000/0001] [00:00:39.6] compute a_g
[0000/0001] [00:02:21.1] Computed Voronoi decomposition grid
[0000/0001] [00:02:21.1] Start
[0000/0001] [00:03:15.7] Computed LCAO weights for projection [201, 202]
[0000/0001] [00:03:15.7] Gather P_ani
[0000/0001] [00:03:15.7] Done gathering
[0000/0001] [00:03:15.7] Distribute C_nM and P_ani
[0000/0001] [00:03:15.8] Done distributing
[0000/0001] [00:03:15.8] Distributed vt_MM
[0000/0001] [00:03:19.4] Calculated vt_nn in parallel
[0000/0001] [00:03:19.5] Distributed vt_nn
[0000/0001] [00:03:19.5] Calculated correction
Written voronoi.ulm

from rhodent.response  import ResponseFromWaveFunctions
from rhodent.calculators import HotCarriersCalculator
from rhodent.voronoi import VoronoiReader

# Set up the density matrices object
response = ResponseFromWaveFunctions(
    ksd='ksd.ulm',
    wfs_fname='wfs_gauss.ulm')

# Set up the Voronoi file reader
voronoi = VoronoiReader('voronoi.ulm')

# Set up the hot-carriers calculator that calculates and broadens dipole contributions onto an energy grid
calc = HotCarriersCalculator(response,
                             times=[30000],
                             voronoi=voronoi,
                             energies_occ=np.arange(-5, 1, 0.01),
                             energies_unocc=np.arange(-1, 5, 0.01),
                             sigma=0.07)

# Calculate the hot carrier distributions and save them to a file
calc.calculate_hcdist_and_write('hcdist_gauss_proj.dat', average_times=False)

[0000/0001] [00:00:00.0] Opened item #0
[0000/0001] [00:00:00.1] Opened item #100
[0000/0001] [00:00:00.3] Set up calculator:
============ HotCarriersCalculator =============
response:
  ResponseFromWaveFunctions
    ksd: ksd.ulm
    wfs_fname: wfs_gauss.ulm
    perturbation:
      No perturbation

voronoi:
  VoronoiReader for ground state with 3626 bands
  1 projections:
    #0  : On atoms [201, 202]

Energies for broadening (sigma = 0.1 eV)
  Occupied: 600 from -5.0 to 1.0 eV
  Unoccupied: 600 from -1.0 to 5.0 eV
------------------------------------------------
[0000/0001] [00:00:00.4] Will use 0.0MiB per rank (total 0.0GiB on 1 ranks)
[0000/0001] [00:00:00.5] (on 1 ranks) Constructing C0_sknM
[0000/0001] [00:00:22.1] (on 1 ranks) Constructed C0_sknM
[0000/0001] [00:00:22.1] (on 1 ranks) Constructing rho0_skMM
[0000/0001] [00:00:35.2] (on 1 ranks) Constructed rho0_skMM
[0000/0001] [00:00:44.7] Calculated and broadened HC distributions in 44.65s for 29820.0as
[0000/0001] [00:00:44.7] Finished calculating hot-carrier matrices
Written hcdist_gauss_proj.dat

!head hcdist_gauss_proj.dat

# Hot carrier (H=hole, E=electron) distributions relative to Fermi level
# Computed for the following 1 times (in fs)
#   29.8200
# Atomic projections
#      0: [201, 202]
# Gaussian folding, Width 0.0700eV
# H energy (eV)   E energy (eV)     Total H (1/eV)     Total E (1/eV)   Proj H  0 (1/eV)   Proj E  0 (1/eV)  ... repeated for next times
      -5.000000       -1.000000     2.55043922e-10     1.52320464e-46    -6.09450410e-12     6.55560423e-50
      -4.990000       -0.990000     2.59895514e-10     1.02547007e-45    -6.18097018e-12     4.41197201e-49
      -4.980000       -0.980000     2.64727071e-10     6.76465395e-45    -6.29340337e-12     2.90941670e-48

from matplotlib import pyplot as plt

data = np.loadtxt('hcdist_gauss_proj.dat')

energies_occ = data[:, 0]
energies_unocc = data[:, 1]

fig, axes = plt.subplots(2, 2, sharey='row', sharex='col', figsize=(6, 3), dpi=200)

axes[0, 0].plot(energies_occ, data[:, 2])
axes[0, 1].plot(energies_unocc, data[:, 3])
axes[1, 0].plot(energies_occ, data[:, 4])
axes[1, 1].plot(energies_unocc, data[:, 5])

axes[0, 0].set_ylabel('Total carriers (1/eV)')
axes[1, 0].set_ylabel('Carriers on \n molecule (1/eV)')
axes[-1, 0].set_xlabel('Energy holes (eV)')
axes[-1, 1].set_xlabel('Energy electrons (eV)')

fig.tight_layout()

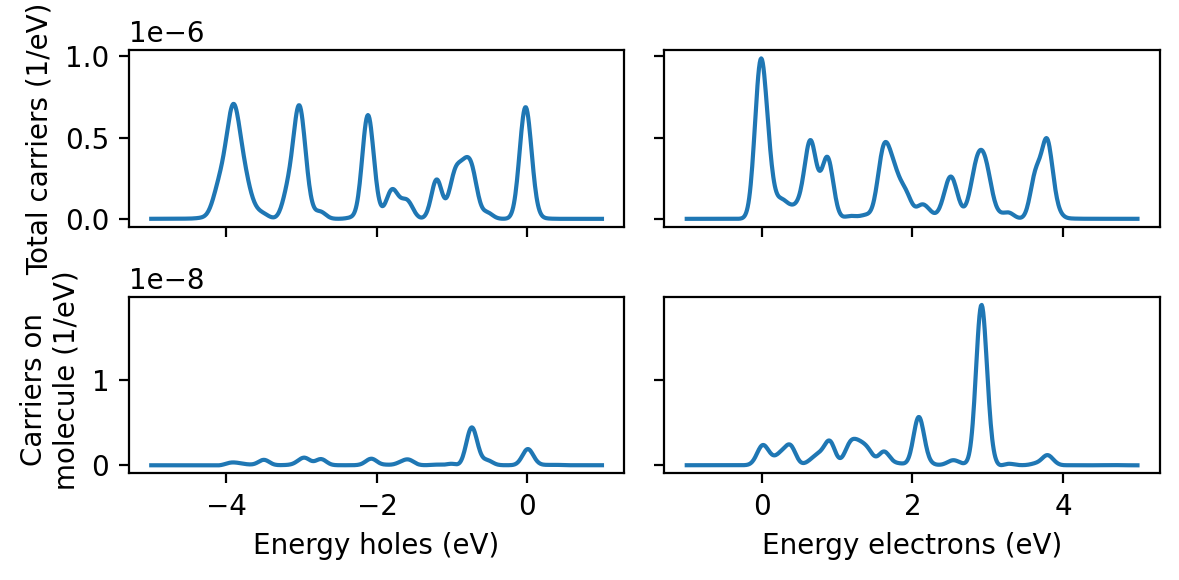
Obtaining the total number of carriers

If we are not interested in hot-carrier distributions, but only the total number of generated carriers in the respective regions, then we can use the calculate_hcsweeptime_and_write function instead.

import numpy as np
from rhodent.response import ResponseFromWaveFunctions
from rhodent.calculators import HotCarriersCalculator
from rhodent.voronoi import VoronoiReader

# Set up the density matrices object
response = ResponseFromWaveFunctions(
    ksd='ksd.ulm',
    wfs_fname='wfs_gauss.ulm')

# Set up the Voronoi file reader
voronoi = VoronoiReader('voronoi.ulm')

# Set up the hot-carriers calculator that calculates and broadens dipole contributions onto an energy grid
calc = HotCarriersCalculator(response,
                             times=np.arange(0, 30e3, 100),
                             voronoi=voronoi)

# Calculate the hot carrier distributions and save them to a file
calc.calculate_hcsweeptime_and_write('hcdist_gauss_time.dat')

!head hcdist_gauss_time.dat

# Hot carrier (H=hole, E=electron) numbers
#
# Atomic projections:
#      0: [201, 202]
#
#       Time (fs)         Total H         Total E       Proj H  0       Proj E  0
         0.020000  2.72573372e-19  2.72573372e-19  2.27957876e-21  3.84953606e-21
         0.220000  5.19251063e-17  5.19251063e-17  3.22714986e-19  7.63459641e-19
         0.420000  4.05332005e-17  4.05332005e-17  1.75037592e-19  7.18875379e-19
         0.620000  3.41373472e-16  3.41373472e-16  1.78031882e-18  3.53014396e-18

import numpy as np
from matplotlib import pyplot as plt

data = np.loadtxt('hcdist_gauss_time.dat')

time = data[:, 0]

fig, axes = plt.subplots(3, 1, sharey='row', sharex='col', figsize=(6, 4), dpi=200)

axes[0].plot(time, pulse.strength(time * fs_to_au))
axes[1].plot(time, data[:, 2])
axes[2].plot(time, data[:, 4], label='Electrons')
axes[2].plot(time, data[:, 3], label='Holes')

axes[0].set_ylabel('Pulse')
axes[1].set_ylabel('Total carriers')
axes[2].set_ylabel('Carriers on \n molecule')
axes[2].legend()
axes[-1].set_xlabel('Time (fs)')

fig.tight_layout()

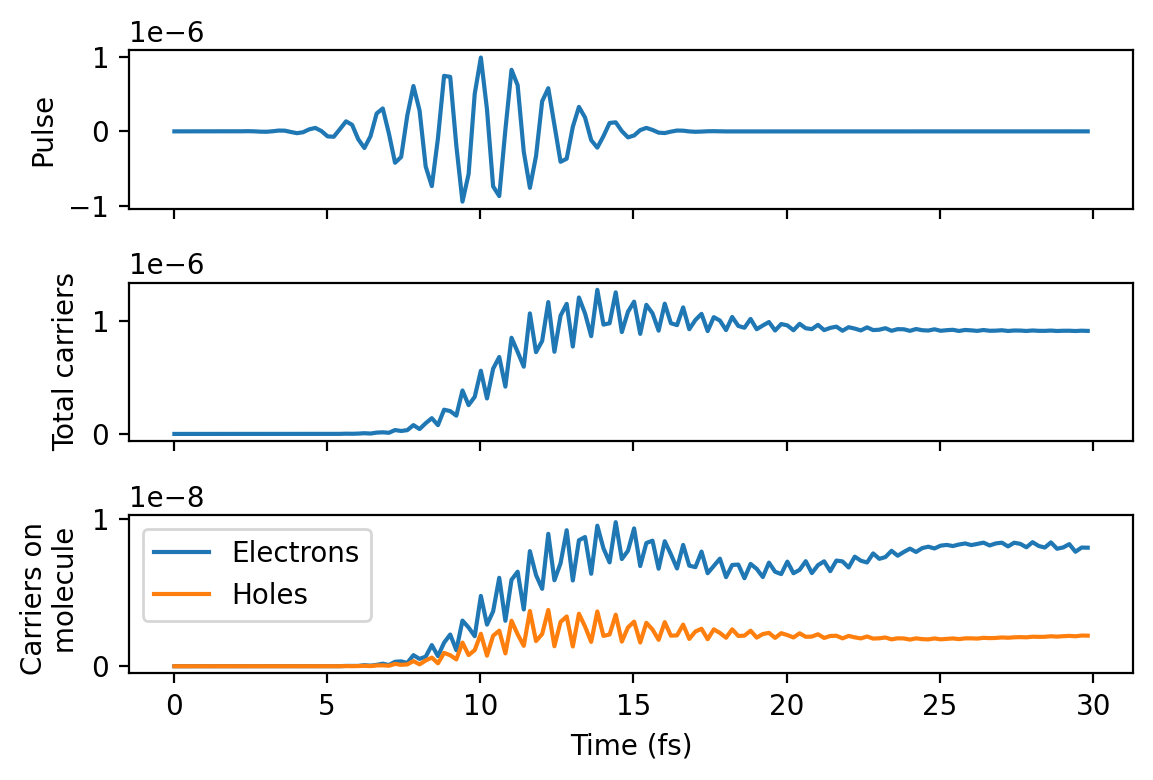
References

• 13. Kuisma, A. Sakko, T. P. Rossi, A. H. Larsen, J. Enkovaara, L. Lehtovaara, and T. T. Rantala, Localized surface plasmon resonance in silver nanoparticles: Atomistic first-principles time-dependent density-functional theory calculations, Phys. Rev. B 91, 115431 (2015).