The convolution trick
The purpose of this page is to show that responses to arbitrary pulses are related to each other, as long as the response is in the linear regime, and the pulses overlap in frequency. We can take advantage of this relation by performing one expensive TDDFT calculation with a pulse that has a broad spectral response (like a delta-kick or sinc-shaped pulse), and in post-processing obtain the response to any other pulse.
To perform the exercises, we need the following files, that are obtained by following the steps in Preparations.
ksd.ulm- KohnShamDecomposition filewfs.ulm- Time-dependent wave functions file after excitation by sinc-shaped pulsedm.dat- Dipole moment file after excitation by sinc-shaped pulsewfs_delta.ulm- Time-dependent wave functions file after excitation by delta-kickdm_delta.dat- Dipole moment file after excitation by delta-kickwfs_gauss.ulm- Time-dependent wave functions file after excitation by Gaussian pulsedm_gauss.dat- Dipole moment file after excitation by Gaussian pulse
We will also need the following files from the Getting started tutorial.
voronoi.ulm- File with Voronoi weightshcdist_proj.dat- Data file with projected hot-carrier distributions
Plotting the perturbations
Let plot the three different perturbations used in the TDDFT calculations, in the time and frequency domains. We set up Perturbation objects for this purpose.
The
amplitudemethod returns the perturbation in the time domain, for a grid of times in atomic units.The
frequenciesmethod returns a grid of frequencies in atomic units. As arguments, it takes a grid of times, and a data length. By supplying a length that is longer than the time grid, the frequencies grid is made more dense.The
fouriermethod returns the Fourier transform of the perturbation, given a grid of times and data length.
Internally, these objects use the fft module of numpy to take the Fourier transform. By working with real data in the time domain, only the positive frequency axis of the Fourier transform is needed.
When plotting, we convert from atomic units of time to femtoseconds and atomic units of frequency to electron volts by multiplying the grids with the conversion factors au_to_fs and au_to_eV.
[ ]:
import numpy as np
from matplotlib import pyplot as plt
from gpaw.tddft.units import au_to_fs, au_to_eV
# Set up a dense time grid in atomic units
times = np.linspace(0, 1200, 500)
timestep = times[1] - times[0]
# Specify a number of data samples that is longer than our data,
# causing our data to be zero padded before Fourier transformation.
# For now, this is for visualization purposes only, but later we
# will do this to break the periodicity of the Fourier transform.
padnt = 2 * len(times) # Number of times, including zero padding
def plot(perturbation, exp):
fig, axes = plt.subplots(1, 2, figsize=(6, 2.4))
# Pulse in the time domain
pulse_amplitudes = perturbation.amplitude(times)
scale = 10**(-exp)
axes[0].plot(times * au_to_fs, scale * pulse_amplitudes)
axes[0].set(xlabel='Time (fs)', ylabel=fr'Amplitude $\times 10^{{{exp}}}$')
# Pulse in the frequency domain
frequencies = perturbation_sinc.frequencies(times, padnt)
pulse_fourier = perturbation.fourier(times, padnt)
axes[1].plot(frequencies * au_to_eV, scale * pulse_fourier.real, label='Re')
axes[1].plot(frequencies * au_to_eV, scale * pulse_fourier.imag, label='Im')
axes[1].plot(frequencies * au_to_eV, scale * np.abs(pulse_fourier), label='Abs',
color='k', lw=1)
axes[1].set(xlabel='Frequency (eV)', xlim=[0, 10])
fig.tight_layout()
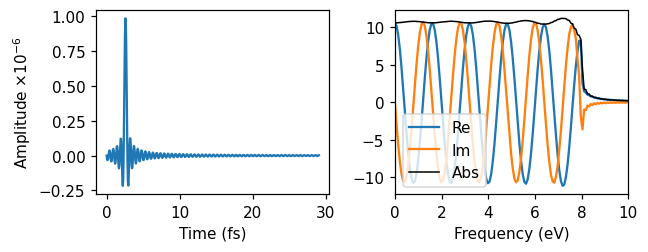
Sinc-shaped pulse
First, we ran real-time TDDFT with a sinc-shaped pulse. The parameters are chosen such that the amplitude, in the time domain, is close to zero in the beginning of the simulation. The maximum amplitude occurs after 5 oscillations. In the frequency domain, the absolute value of the pulse is relatively constant up to 8 eV, where it is smoothly cut off. By perturbing the system with this pulse, we are thus exciting up to 8 eV frequency-components of the response.
[ ]:
from rhodent.perturbation import create_perturbation
# Set up perturbations
perturbation_sinc = create_perturbation(
{'name': 'SincPulse',
'strength': 1e-6, # Amplitude
'cutoff_freq': 8, # Cut-off frequency in units of eV
'time0': 5, # Time of maximum in number of oscillations
'relative_t0': True})
print(perturbation_sinc)
plot(perturbation_sinc, -6)
plt.legend(loc='lower left');
name: SincPulse, strength: 1e-06, time0: 5
cutoff_freq: 8, relative_t0: True
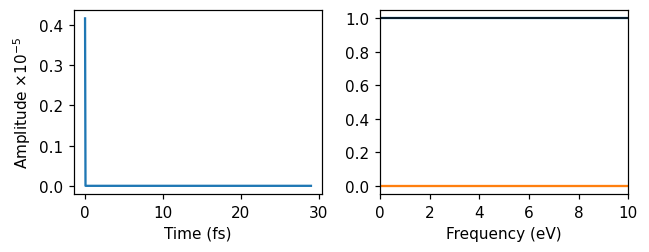
Delta-kick
Then, we used a delta-kick, which is a perturbation that is exacly constant (and real) in frequency space. The strength of the delta kick is specified in the frequency domain to \(10^{-5}\).
[ ]:
perturbation_delta = create_perturbation(
{'name': 'deltakick',
'strength': 1e-5, # Strength in frequency domain
})
print(perturbation_delta)
plot(perturbation_delta, -5)
Delta-kick perturbation (strength 1.0e-05)
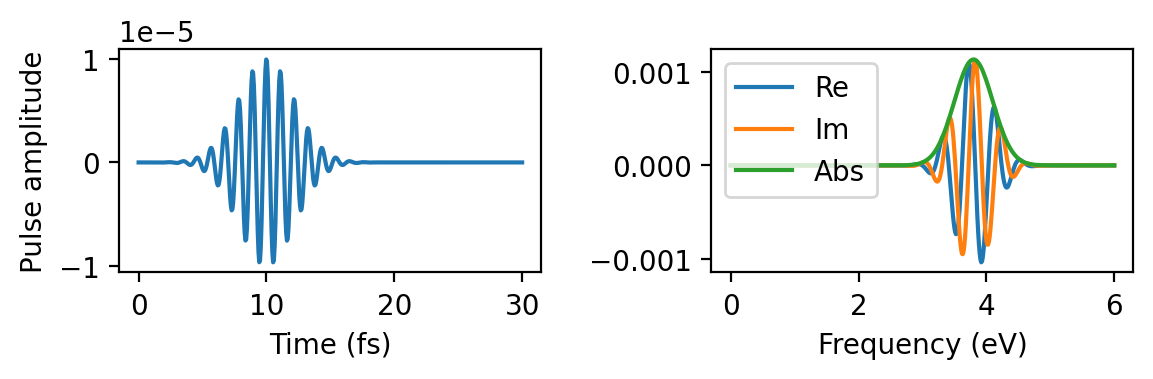
Gaussian pulse
Finally, we used a Gaussian pulse pulse of frequency 3.8 eV with a maximum in the time domain at 10 fs. The sigma parameter (0.3 eV) corresponds to a full width at half-maximum (FWHM) of about 0.7 eV in the frequency domain and 5 fs in the time domain.
[ ]:
perturbation_gauss = create_perturbation(
{'name': 'GaussianPulse',
'strength': 1e-6, # Amplitude
'frequency': 3.8, # Frequency in units of eV
'time0': 10e3, # Time of maximum in units of fs
'sigma': 0.3, # Parameter related to width in frequency domain, in units of eV
'sincos': 'cos'})
print(perturbation_gauss)
plot(perturbation_gauss, -5)
name: GaussianPulse, strength: 1e-06
time0: 10000.0, frequency: 3.8, sigma: 0.3
sincos: cos
Performing the pulse convolution
Now, we will demonstrate how the response to one perturbation can be obtained from the response to another perturbation. As an instructive example, we begin with the dipole moment.
In the linear response regime, we can express the dipole moment \(\boldsymbol{d}\) as the polarizability times the external perturbation in the (spatially constant) electric field. In the frequency domain
or, equivalently, in the time domain
Therefore, if we know the dipole response to one perturbation (e.g. \(\boldsymbol{d}_\mathrm{sinc}\) to a sinc perturbation \(\boldsymbol{E}_\text{sinc}\)), then we know the polarizability (at least at frequencies where the perturbation is non-zero). Hence, we can reconstruct the response to any other perturbation (e.g. \(\boldsymbol{d}_\mathrm{gauss}\) to a Gaussian laser field \(\boldsymbol{E}_\text{gauss}\)). This is most easily obtained in frequency space
The polarizability is a 3x3 tensor and its full calculation requires three separate TDDFT calculations with perturbations in different directions. For simplicity, we will assume that the perturbations of interest for us are in the same direction, and we can thus use the scalar amplitudes \(v(\omega)\) of the perturbations.
Read and plot the dipole moment
First, we read the dipole moment files dm.dat, dm_delta.dat containing \(\boldsymbol{d}_\text{sinc}(t)\), and \(\boldsymbol{d}_\text{delta}(t)\).
[ ]:
from gpaw.tddft.units import au_to_eA
def read_dipole_file(filename):
""" Read dipole moment file.
Return the time (in atomic units) and the
z-component of the dipole moment (in units of eÅ).
Discard step-like data, and repeated data due to restarts.
Subtract the static dipole.
"""
# Read dipole moment file and subtract static dipole
time_t, _, _, _, dm_t = np.loadtxt(filename, unpack=True)
dm_t -= dm_t[0]
dm_t *= au_to_eA # Convert from atomic units to eÅ
# Remove any non-increasing times (due to restart of kick)
flt_t = np.ones_like(time_t, dtype=bool)
maxtime = time_t[0]
for t in range(1, len(time_t)):
if time_t[t] > maxtime:
maxtime = time_t[t]
else:
flt_t[t] = False
time_t = time_t[flt_t]
dm_t = dm_t[flt_t]
return time_t, dm_t
# Read times and dipole moments in atomic units
times_sinc, dipole_moments_sinc = read_dipole_file('dm.dat') # After sinc-pulse
times_delta, dipole_moments_delta = read_dipole_file('dm_delta.dat') # After delta-kick
# Plot
fig, ax = plt.subplots(1, 1, figsize=(6, 3))
ax.plot(times_sinc * au_to_fs, dipole_moments_sinc, label='Sinc-pulse')
ax.plot(times_delta * au_to_fs, dipole_moments_delta, label='Delta-kick')
ax.set(xlabel='Time (fs)', ylabel=r'Dipole moment (eÅ)')
ax.legend(loc='upper right', fontsize=8)
fig.tight_layout()
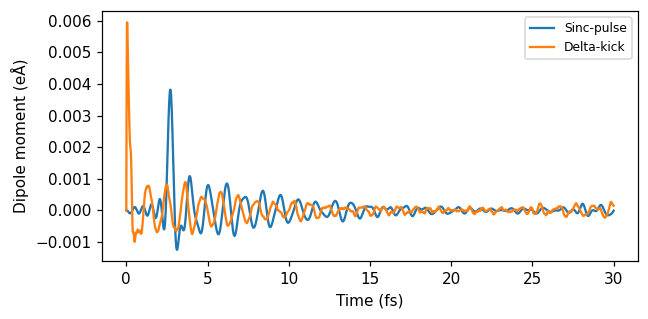
Then, we compute the polarizability from the sinc response
and from the delta-kick response
using normalize_frequency_response. This function takes the Fourier transform of the data (\(\boldsymbol{d}(t)\)) and the perturbation (\(v(t)\)) and performs the division. The resuling response is set to zero for frequencies where the perturbation is close to zero, to avoid numerical noise.
We plot the real part of the polarizability obtained from both sources, to see that the agreement is excellent below the cut-off of the sinc-pulse of 8 eV. Above 8 eV we are starting to see numerical noise due to the strength of the perturbation being low.
[ ]:
from gpaw.tddft.units import au_to_as, au_to_eV
padnt = 2 * len(times_sinc) # Number of times, including zero padding
# Frequencies grid (same for both perturbations)
frequencies = perturbation_sinc.frequencies(times_sinc, padnt)
normalized_dipole_fourier_sinc = perturbation_sinc.normalize_frequency_response(
dipole_moments_sinc, times_sinc, padnt)
normalized_dipole_fourier_delta = perturbation_delta.normalize_frequency_response(
dipole_moments_delta, times_delta, padnt)
# Plot
fig, ax = plt.subplots(1, 1, figsize=(6, 2.4))
ax.plot(frequencies * au_to_eV, normalized_dipole_fourier_sinc.real, label='Sinc-pulse')
ax.plot(frequencies * au_to_eV, normalized_dipole_fourier_delta.real, label='Delta-kick')
ax.set(xlabel='Frequency (eV)', ylabel='Polarizability', xlim=[0, 10])
ax.legend(loc='upper right', fontsize=8)
fig.tight_layout()
Finally, we multiply the polarizability by the Gaussian perturbation in the frequency domain
and
[ ]:
fig, ax = plt.subplots(1, 1, figsize=(6, 2.4))
fourier_gauss = perturbation_gauss.fourier(times_sinc, padnt)
dipole_fourier_conv_sinc = normalized_dipole_fourier_sinc * fourier_gauss
dipole_fourier_conv_delta = normalized_dipole_fourier_delta * fourier_gauss
ax.plot(frequencies * au_to_eV, dipole_fourier_conv_sinc.real, label='Sinc-pulse')
ax.plot(frequencies * au_to_eV, dipole_fourier_conv_delta.real, label='Delta-kick')
ax.set(xlabel='Frequency (eV)', ylabel='Dipole moment', xlim=[0, 10])
ax.legend(loc='upper right', fontsize=8)
fig.tight_layout()
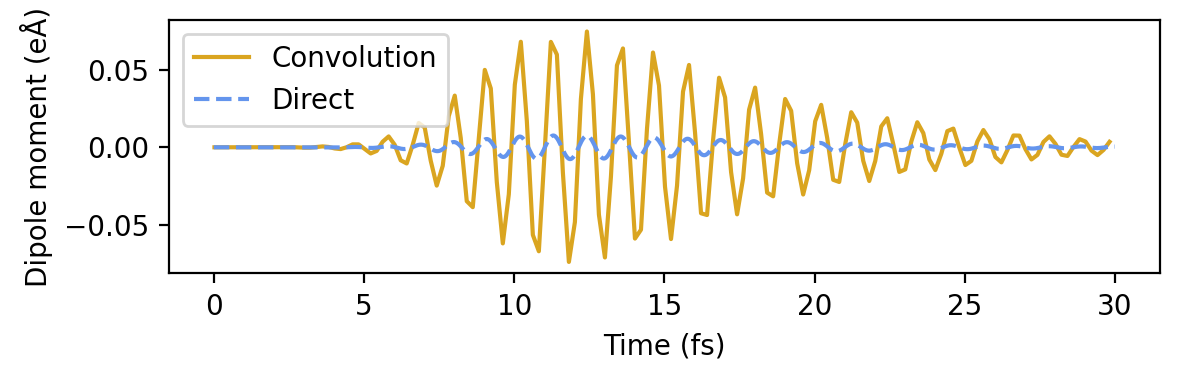
and take the inverse Fourier transform the obtain the dipole moment due to the Gaussian pulse. Plotting this quantity obtained from the sinc-pulse and delta-kick calculations, against the dipole moment from the actual Gaussian pulse calculation shows excellent agreement.
[ ]:
dt = times_sinc[1] - times_sinc[0] # Time step in atomic units
conv_from_sinc = np.fft.irfft(dipole_fourier_conv_sinc, n=padnt)[:len(times_sinc)] / dt
conv_from_delta = np.fft.irfft(dipole_fourier_conv_delta, n=padnt)[:len(times_delta)] / dt
# Read dipole moment from Gaussian pulse
times_gauss, dipole_moments_gauss = read_dipole_file('dm_gauss.dat')
# Plot
fig, ax = plt.subplots(1, 1, figsize=(6, 2.4))
ax.plot(times_sinc * au_to_fs, conv_from_sinc, label='Sinc-pulse convolution')
ax.plot(times_delta * au_to_fs, conv_from_delta, '-.', label='Delta-kick convolution')
ax.plot(times_gauss * au_to_fs, dipole_moments_gauss, '--', label='Gaussian pulse')
ax.set(xlabel='Time (fs)', ylabel=r'Dipole moment (eÅ)')
ax.legend(loc='lower left', fontsize=8)
fig.tight_layout()
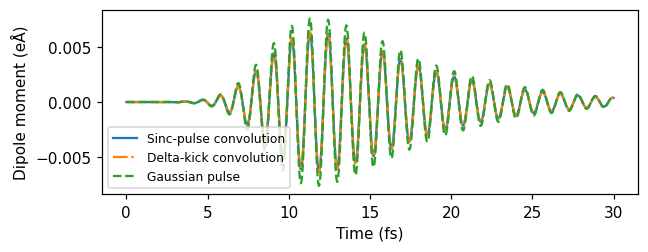
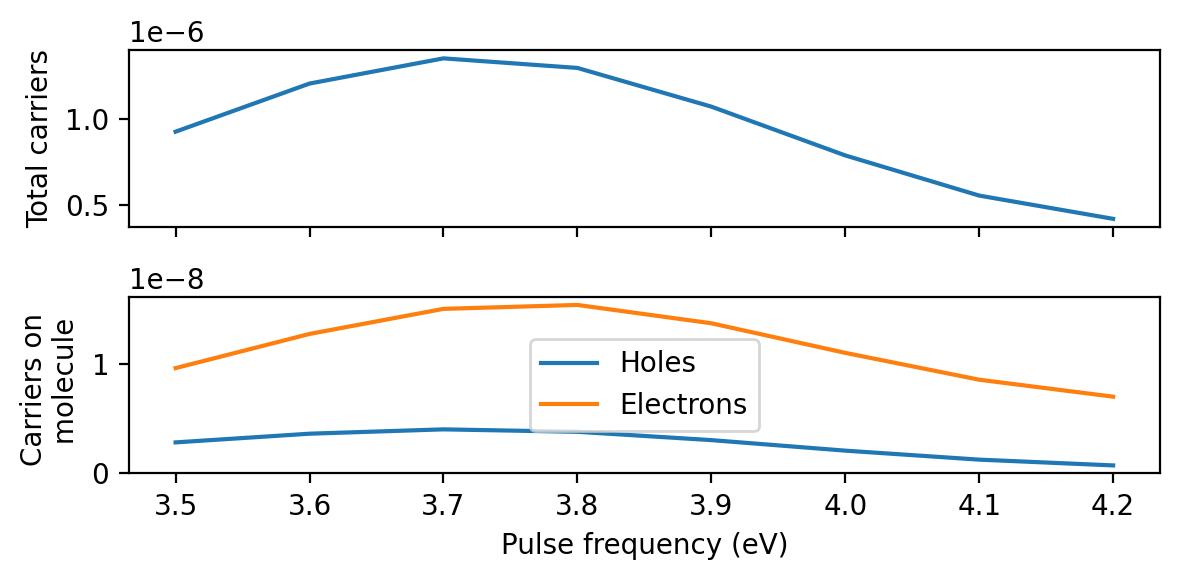
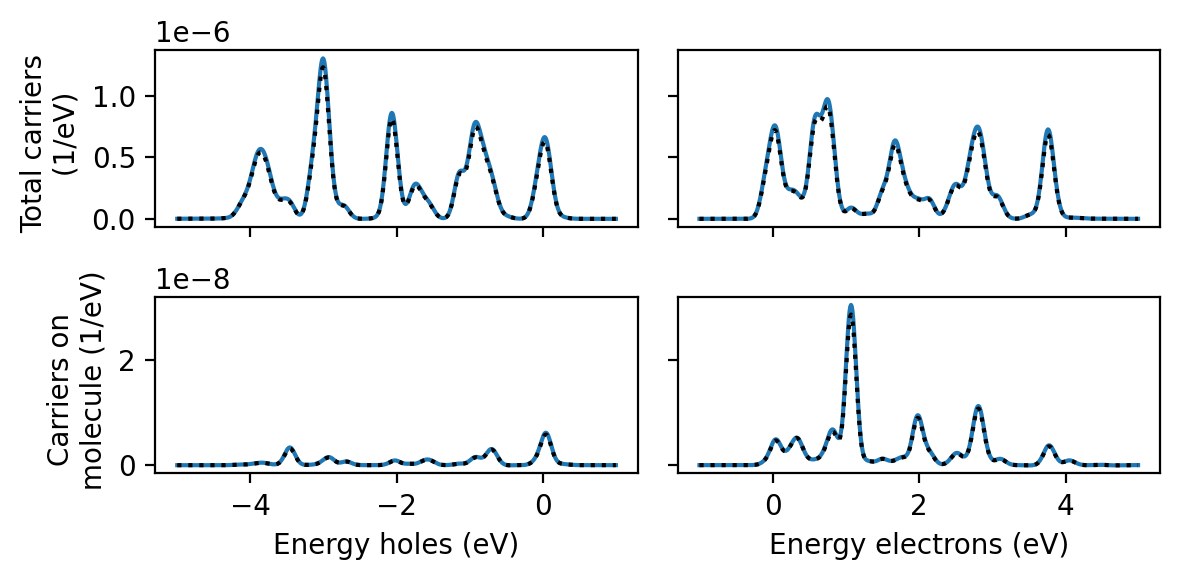
Obtaining projected hot-carrier distributions
The same principle applies to any other quantity which is linear in the perturbation, including the electron-hole part of the KS density matrix
We obtain projected hot-carrier distributions just like in the Getting started tutorial, with the only difference that we provide a different perturbation parameter to our ResponseFromWaveFunctions. Compared to the sinc-pulse convolution, the pulse convolution using the delta kick is drastically more expensive because the time step in the time-dependent wave functions file is 10 times shorter.
To calculate the hot-carrier distributions using the Gaussian-pulse response directly, we simply specify a perturbation=None as well as pulses=[None]. This tells rhodent to read density matrices without performing pulse convolution. This is cheap enough to run in a few minutes on a single core.
In all cases, the agreement is very good.
[ ]:
import numpy as np
from rhodent.response import ResponseFromWaveFunctions
from rhodent.calculators import HotCarriersCalculator
from rhodent.voronoi import VoronoiReader
# Set up the perturbation used in the TDDFT calculation
perturbation = {'name': 'deltakick', 'strength': 1e-5}
response = ResponseFromWaveFunctions(wfs_fname='wfs_delta.ulm',
ksd='ksd.ulm',
perturbation=perturbation)
# Set up the Gaussian pulse that we want to know the response for
pulse = {'name': 'GaussianPulse', 'strength': 1e-6,
'frequency': 3.8, 'time0': 10e3, 'sigma': 0.3}
# Load the Voronoi weights
voronoi = VoronoiReader('voronoi.ulm')
# Set up the calculator
calc = HotCarriersCalculator(response=response,
voronoi=voronoi,
energies_occ=np.arange(-5, 1.001, 0.01),
energies_unocc=np.arange(-1, 5.001, 0.01),
sigma=0.07,
times=np.linspace(25e3, 30e3, 10),
pulses=[pulse])
# Calculate the energies
calc.calculate_distributions_and_write('hcdist_proj_delta.dat')
[ ]:
import numpy as np
from rhodent.response import ResponseFromWaveFunctions
from rhodent.calculators import HotCarriersCalculator
from rhodent.voronoi import VoronoiReader
# Set up a response without a perturbation specified
response = ResponseFromWaveFunctions(wfs_fname='wfs_gauss.ulm',
ksd='ksd.ulm',
perturbation=None)
# Load the Voronoi weights
voronoi = VoronoiReader('voronoi.ulm')
# Set up the calculator, without specifying a pulse
# No pulse convolution will be performed
calc = HotCarriersCalculator(response=response,
voronoi=voronoi,
energies_occ=np.arange(-5, 1.001, 0.01),
energies_unocc=np.arange(-1, 5.001, 0.01),
sigma=0.07,
times=np.linspace(25e3, 30e3, 10))
# Calculate the energies
calc.calculate_distributions_and_write('hcdist_proj_gauss.dat')
### #####
###############
######## ##### ##
########### ### _ _ _
####### ### _ __| |__ ___ __| | ___ _ __ | |_
#### ## | '__| '_ \ / _ \ / _` |/ _ \ '_ \| __|
# ## | | | | | | (_) | (_| | __/ | | | |_
# ## |_| |_| |_|\___/ \__,_|\___|_| |_|\__| 0.1
# ##
# ##
## ###
#### ###
########## ##
######## ###
### ####
## ####
## ######
#################
Date: Mon Jun 9 21:41:02 2025
CWD: /home/jakub/proj/rhodent-supplementary/notebooks/pulse_convolution
cores: 1
Python: 3.12.3
numpy: /home/jakub/git/auto-venv-setup/venv/gpaw/upstream/lib/python3.12/site-packages/numpy (version 1.26.4)
ASE: /home/jakub/git/ase/ase (version 3.25.0b1)
GPAW: /home/jakub/git/gpaw/upstream/gpaw (version 25.1.1b1)
[00:00:00.0] [Reader] Opening time-dependent wave functions file wfs_gauss.ulm
[00:00:00.0] [Reader] Opened time-dependent wave functions file with 150 times
[00:00:00.1] Set up calculator:
=========== HotCarriersCalculator ============
response:
ResponseFromWaveFunctions
ksd: ksd.ulm
wfs_fname: wfs_gauss.ulm
perturbation:
No perturbation
voronoi:
VoronoiReader for ground state with 3626 bands
1 projections:
#0 : On atoms [201, 202]
Energies for broadening (sigma = 0.1 eV)
Occupied: 601 from -5.0 to 1.0 eV
Unoccupied: 601 from -1.0 to 5.0 eV
------------------------------------------------
==================================
Procedure for obtaining response
==================================
Response from time-dependent wave functions
Time-dependent wave functions reader
Constructing density matrices in basis of ground state orbitals.
file: wfs_gauss.ulm
wave function dimensions (1310, 3626)
10 times
25020.0, 25620.0, 26020.0, ..., 29820.0 as
1 ranks reading in 10 iterations
Density matrix shape (1123, 2521)
reading real and imaginary parts
=================
Memory estimate
=================
Voronoi weights ii: (1, 1123, 1123) float64
. 9.6 MiB per rank on 1 ranks
. 9.6 MiB in total on all ranks
Voronoi weights aa: (1, 2521, 2521) float64
. 48.5 MiB per rank on 1 ranks
. 48.5 MiB in total on all ranks
Reading response:
Density matrix: (1123, 2521, 2) float64
. 43.2 MiB per rank on 1 ranks
. 43.2 MiB in total on all ranks
Time-dependent wave functions reader:
C0S_nM: (1310, 3626) float64
. 36.2 MiB per rank on 1 ranks
. 36.2 MiB in total on all ranks
rho0_MM: (3626, 3626) float64
. 100.3 MiB per rank on 1 ranks
. 100.3 MiB in total on all ranks
........................
.. Total on all ranks ..
.......136.6 MiB........
........................
.. Total on all ranks ..
.......179.7 MiB........
........................
.. Total on all ranks ..
.......237.9 MiB........
[00:00:00.2] [Reader] Constructing C0_sknM on 1 ranks
[00:00:21.8] [Reader] Constructed C0_sknM
[00:00:21.8] [Reader] Constructing rho0_skMM on 1 ranks
[00:00:34.8] [Reader] Constructed rho0_skMM
[00:00:39.7] [Calculator] Calculated and broadened HC distributions in 39.66s for 25020.0as
[00:00:44.4] [Calculator] Calculated and broadened HC distributions in 44.44s for 25620.0as
[00:00:49.1] [Calculator] Calculated and broadened HC distributions in 49.08s for 26020.0as
[00:00:53.7] [Calculator] Calculated and broadened HC distributions in 53.70s for 26620.0as
[00:00:58.3] [Calculator] Calculated and broadened HC distributions in 58.34s for 27220.0as
[00:01:03.0] [Calculator] Calculated and broadened HC distributions in 62.97s for 27820.0as
[00:01:07.6] [Calculator] Calculated and broadened HC distributions in 67.60s for 28420.0as
[00:01:12.2] [Calculator] Calculated and broadened HC distributions in 72.23s for 28820.0as
[00:01:16.9] [Calculator] Calculated and broadened HC distributions in 76.86s for 29420.0as
[00:01:21.5] [Calculator] Calculated and broadened HC distributions in 81.51s for 29820.0as
[00:01:21.5] [Calculator] Finished calculating hot-carrier matrices
[00:01:21.5] [Calculator] Written hcdist_proj_gauss.dat
[ ]:
from matplotlib import pyplot as plt
data_sinc = np.loadtxt('hcdist_proj.dat')
data_delta = np.loadtxt('hcdist_proj_delta.dat')
data_gauss = np.loadtxt('hcdist_proj_gauss.dat')
fig, axes = plt.subplots(2, 1, sharex=True, figsize=(6, 4.5))
scale = 1e8
axes[0].plot(data_sinc[:, 1], scale * data_sinc[:, 3], '-')
axes[1].plot(data_sinc[:, 1], scale * data_sinc[:, 5], '-', label='Sinc-pulse convolution')
axes[0].plot(data_delta[:, 1], scale * data_delta[:, 3], '-.')
axes[1].plot(data_delta[:, 1], scale * data_delta[:, 5], '-.', label='Delta-kick convolution')
axes[0].plot(data_gauss[:, 1], scale * data_gauss[:, 3], '--')
axes[1].plot(data_gauss[:, 1], scale * data_gauss[:, 5], '--', label='Gauss response')
axes[1].legend(loc='upper left', fontsize=8)
axes[0].set_ylabel('Total carriers ($10^{-8}$/eV)')
axes[1].set_ylabel('Carriers on molecule\n($10^{-8}$/eV)')
axes[-1].set_xlabel('Energy (eV)')
fig.tight_layout()